 |
Atelier "Effet Doppler - Cosmologie"
Cet atelier est fourni comme base pour l'étude de la notion de l'effet Doppler inscrite au nouveau programme officiel de terminal S (Bulletin Officiel spécial n°8 du 13 octobre 2011) p. 7
Programme/
Observer/ Ondes et Matière/ Caractéristiques et
propriétés des ondes/ Effet Doppler
Effet Doppler :
Mettre en
oeuvre une démarche expérimentale pour mesurer une vitesse en
utilisant l’effet Doppler. Exploiter l’expression
du
décalage Doppler de la fréquence dans le cas des faibles vitesses.
Utiliser des données spectrales et un logiciel de traitement
d’images pour illustrer l’utilisation de
l’effet
Doppler comme moyen d’investigation en astrophysique.
Mesurer l'âge de l'univers
Objectif
et méthode
Hubble et les
galaxies
L'expansion de
l'univers
L'effet Doppler
Le spectre des
galaxies
Les unités
Procédure
à suivre
La loi de Hubble
L'âge de
l'Univers
COMPLEMENTS
- L’interprétation
de
l’expansion de l’Univers
- La
détermination exacte de
l’âge de l’Univers
- L’accélération
de
l’expansion
SOURCES
LIENS EXTERNES
Pour télécharger le dossier en PDF : Age_de_univers.pdf (1.8 Mo)
 Objectif et
Méthode
Objectif et
Méthode
Méthode : A partir d’un échantillon réel de galaxies, évaluer par l’effet Doppler la vitesse apparente d’éloignement des galaxies. Par comparaison avec la distance fournie de ces galaxies, calculer le taux d’expansion de l’Univers (constante de Hubble) et en déduire une estimation de l’âge de l’Univers.
 Hubble et les
galaxies
Hubble et les
galaxies
La mise en service des premiers grands télescopes dévoile dans le ciel la présence de nébuleuses, régions lumineuses diffuses, qui se révèlent en fait une collection d’étoiles.
Ces nébuleuses provoquent en 1920 un grand débat. Font-elles partie avec notre Voie lactée d’un seul et même ensemble ou sont-elles des ilots d’étoiles totalement séparés ?
Les premières mesures de distance vont trancher. Elles sont beaucoup plus loin que les étoiles qui nous environnent
Ces ilots lointains d’aspect « laiteux » sur le ciel sont baptisés galaxies (du grec galaktikos, laiteux). C’est la mesure de la distance et de la vitesse de ces galaxies qui a permis à l’astronome Hubble de démontrer l’expansion de l’univers
 |
 |
 L'expansion de
l'univers
L'expansion de
l'univers
C’est le soviétique Alexander Friedmann qui découvrit en 1922 que, sans cette constante cosmologique, l’univers prédit par la Relativité générale devait être en expansion.
En mesurant pour la première fois tout à la fois la distance et simultanément la vitesse sur la ligne de visée d’un échantillon de 24 galaxies, Edwin Hubble découvrit en 1929 que plus une galaxie est loin, plus sa vitesse d’éloignement est élevée. Il constate qu’en reportant la vitesse des galaxies en fonction de leur distance, les points se répartissent approximativement le long d’une droite.
Cette proportion régulière entre distance et vitesse est désormais connue sous le nom de « loi de Hubble ». La constante de proportionnalité entre distance et vitesse (la pente de la droite) est la « constante de Hubble »
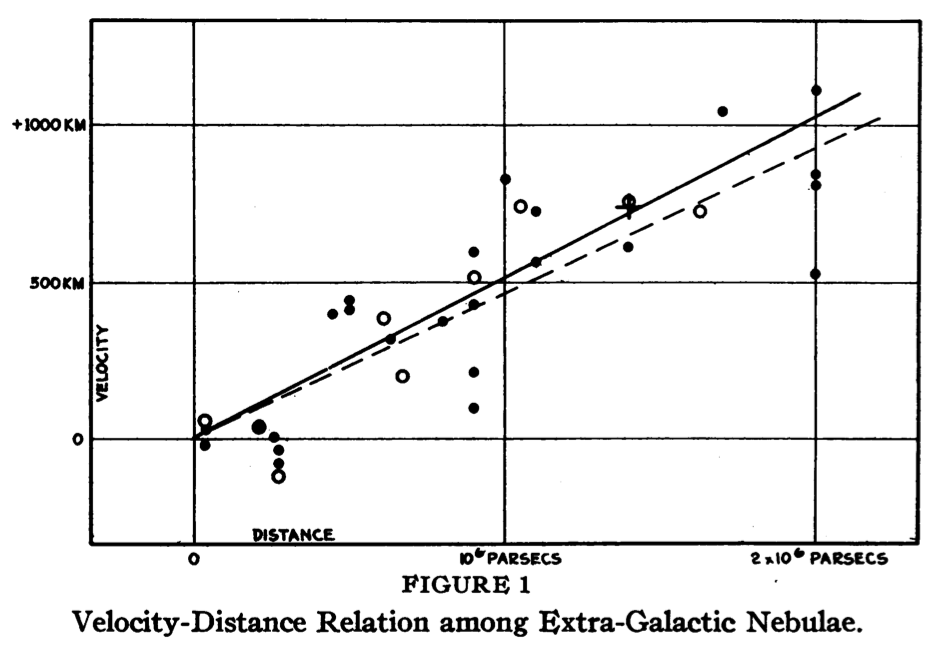 |
(tiré de Proc. Nat. Astron. Soc., vol. 15, p. 168, 1929)
 L'effet Doppler
L'effet Doppler
L’effet Doppler (ou Doppler-Fizeau du nom de ses deux découvreurs) traduit le décalage de longueur d’onde (ou de fréquence) lorsque une onde est reçue en provenance d’un corps en mouvement.
Il peut être montré que ce décalage est proportionnel à la vitesse du corps et dépend du sens du mouvement. Si le corps s’éloigne, la longueur d’onde d'une lumière visible est décalée vers le rouge (la fréquence diminue), s’il se rapproche, elle est décalée vers le bleu (la fréquence augmente).
 |
Un exemple courant est la sirène des pompiers dont le son parait plus aigu (fréquence plus élevée) lorsqu’elle se rapproche et plus grave (fréquence moins élevée) lorsqu’elle s’éloigne
La relation Doppler
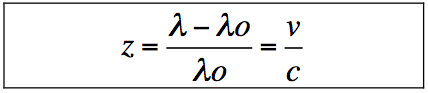 |
λ longueur d’onde mesurée (corps en mouvement)
λo longueur d’onde mesurée (corps immobile)
v = vitesse du corps
c = vitesse de la lumière (300 000 km/s)
(cette formule n’est exacte que si la vitesse ‘v’ est petite devant la vitesse de la lumière ‘c’)
 Le spectre
des galaxies
Le spectre
des galaxies
La lumière en provenance d’une galaxie peut être décomposée (par un prisme ou un réseau) en un spectre lumineux, une répartition de la lumière en fonction de la longueur d’onde (un analogue de l’arc-en-ciel) ;
Dans ce spectre lumineux, on distingue des « raies » d’absorption ou d’émission qui sont la trace des éléments chimiques. Dans les galaxies, la principale raie d’émission est la raie de l’hydrogène, l’élément le plus abondant.
 |
Le décalage vers le rouge de la galaxie peut être évaluée sur le spectre de la galaxie en mesurant l’écart entre la longueur d’onde de la raie d’émission de l’hydrogène – la position du premier pic (le deuxième pic est dû à l’azote) – et la longueur d’onde connue au laboratoire.
 Les
unités
Les
unités
Pour mesurer les distances, les astronomes utilisent le « parsec »
1 parsec = 1pc= 3,085 677x1016 m, soit environ 3,2616 années-lumière.
Le ‘parsec’ (pour ‘par seconde’) est la distance à laquelle on voit la distance Terre-Soleil (150 millions de kilomètres) sous un angle d’une seconde d’arc
La distance des astres dans l’Univers se détermine de proche en proche en établissant une « échelle de distance ». Un des objectifs principaux du télescope spatial Hubble a été d’améliorer la précision de cette échelle des distances.
Pour déterminer la distance des galaxies lointaines, on peut utiliser différentes méthodes :
- utiliser des étoiles variables (Céphéides)
- utiliser la dimension apparente de la galaxie
- utiliser la dimension de régions gazeuses (régions HII)
- utiliser la brillance de certaines explosions d’étoiles (supernova SNIa)
Il existe encore une très large incertitude sur la distance des galaxies
La distance des galaxies n’est pas ici calculée ici mais fournie.
Longueur d’onde- vitesse
Pour mesurer les longueurs d’onde, les astronomes utilisent les Angströms (Å)
1 Å = 0.0001 micromètre ou 10-10 m
10 000 Å = 1 micromètre = 10-6 m
La longueur d’onde de la raie d’hydrogène (la raie Hydrogène α ou Hα) est au laboratoire :
λo(Hα) = 6562.8 Å
En utilisant la formule Doppler
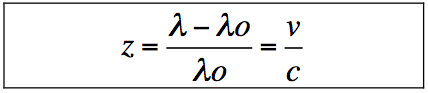
La vitesse de la galaxie peut être calculée à partir du spectre en faisant :

 Procédure
Procédure
Procédure à suivre :
- faire les mesures de la position du pic de la raie 'λmesurée’ en Å
(en mesurant sur la figure du fichier imprimable ou en utilisant le fichier numérique)
- remarquer que le décalage est toujours « vers le rouge » correspondant donc à une vitesse d’éloignement

- calculer la vitesse de la galaxie ‘v’ en km/s avec la formule Doppler
- reporter ces valeurs dans le tableau des galaxies ou utiliser le fichier de saisie EXCEL

 Loi de Hubble
Loi de Hubble
La loi de Hubble établit la proportion entre la distance d’une galaxie et sa vitesse d’éloignement selon la relation :
v (km/s) = Ho . d (Mpc)
Ho est la constante de Hubble, la constante de proportionnalité, exprimée en km/s/Mpc (kilomètre par seconde par Megaparsec)
Méthode
La proportion se traduit par une droite et la constante de Hubble est la pente de la droite.
Comme l’expansion est mesurée depuis le Système solaire, où par convention la vitesse d’éloignement est nulle, la droite doit passer par le point (0,0).

 L'âge de l'Univers
L'âge de l'Univers
v (km/s) = Ho . d (Mpc)
où l'indice 0 de Ho signifie qu’il s’agit de la constante de Hubble au temps de la mesure.
En inversant les termes, elle peut aussi s’écrire :
d(Mpc) = (1/Ho)* v(km/s)
Si on fait l’hypothèse que la valeur de Ho est constante depuis le début de l’expansion, alors la durée de l’expansion peut être calculée en divisant la distance ‘d’ par la vitesse ‘v’ :

L’inverse de la constante de Hubble est donc la durée de l’expansion qui peut être assimilée à l’âge de l’univers.
En réalité, l’expansion n’est pas constante au cours du temps du fait notamment de l’attraction gravitationnelle de la matière qui tend à la ralentir. Pour estimer plus exactement l’âge de l’univers, il est nécessaire d’utiliser les équations de la Relativité générale.
Pour une estimation plus exacte de l’âge de l’univers > voir la détermination exacte
Méthode
Avec les unités astronomiques utilisées, pour calculer l’âge de l’univers, il est nécessaire d’uniformiser les unités de longueur différentes employées pour les distances (Mpc) et les vitesses (km)
- comme 1 Mpc = 1 Megaparsec = 106 pc = 3,09×1019 km
il faut diviser la valeur de Ho (km/s/Mpc) par 3.09×1019 pour obtenir Ho (en km/s/km) soit Ho (en 1/s), c’est à dire l’inverse d’un temps en secondes
(1/Ho), l’inverse de Ho est alors l’âge de l’univers en secondes
- en divisant le résultat par la durée d’une année en secondes (3.16 107s), on obtient l’âge de l’univers en années
Valeur de Hubble (1929)
Reprendre le diagramme originel de Hubble (voir la publication originelle)
Calculer l’âge de l’univers obtenu à partir de ces données (en utilisant la pente de la droite)
On relève pour une distance de d = 2 106 parsecs = 2 Mpc, une vitesse de V = 1000 km/s.
Le valeur approchée de Ho est donc Ho = V/d = 500 km/s/Mpc
Hubble donne deux valeurs Ho=465 et Ho=513 selon qu'il utilise les données individuelles des galaxies ou qu'il choisit de les grouper selon leur distance et position. Remarquez sur le diagramme la présence de plusieurs galaxies à décalage vers le bleu (décalage vers le rouge négatif) et l'erreur de Hubble qui indique "km" et non "km/s" sur son échelle et intervertit dans la légende la signification des deux droites en trait continu et pointillé.
Comparer l'âge déduit de l'univers à l’âge de la Terre.
Les données utilisées par Hubble étaient inexactes en raison d’une sous-estimation systématique de la distance des galaxies. Ce résultat initial a été une des raisons pour lesquelles l’hypothèse d’une expansion de l’univers n’a pas été considérée comme valable jusqu’au milieu du XXe siècle.
 COMPLEMENTS
COMPLEMENTS
D’autres interprétations du décalage vers le rouge ont été proposées comme l’effet de la fatigue de la lumière ou la théorie de la masse variable.
La loi de Hubble est une droite qui passe par l’origine (le point 0,0) mais cela ne signifie pas que l’expansion opère uniquement depuis notre position dans l’espace.
L’hypothèse cosmologique suppose que la même loi de Hubble serait établie par un observateur situé en un point quelconque de l’univers.

La détermination exacte de l'âge de l'Univers
Le calcul exact de l’âge Univers se base actuellement sur la relativité générale (RG).En faisant l’hypothèse d’un univers homogène et isotrope, les équations de la RG, qui décrivent l’interaction de l’espace et de la matière, peuvent être résolues. Elles fournissent un âge de l’univers en fonction de la densité de la matière.
Dans l’hypothèse d’un univers dont la densité de matière est égale à une densité critique, l’âge de l’univers est alors :

L'accélération de l'expansion
Depuis 1998, de nouvelles observations sont venues suggérer que l’expansion subit non seulement l’effet de ralentissement dû à l’attraction de la matière mais un effet d’accélération dû à une hypothétique énergie noire depuis probablement quelques milliards d’années.Cet effet a été établi en prolongeant la loi de Hubble à plus grande distance.
La loi de Hubble à grande distance est établie non grâce des galaxies mais grâce à des explosions d’étoiles très brillantes, les supernovae de type Ia, SNIa, qui sont visibles à très grande distance.
Si cette accélération de l’univers est confirmée, l’âge de l’univers dépend alors non seulement de la densité de matière (notée Ωm) mais aussi de la densité d’énergie noire (notée ΩΛ).


où le facteur correctif f(Ωm et ΩΛ) est évalué ici selon les valeurs de Ωm et ΩΛ

Ωm=0,3 et ΩΛ=0,7 donne f=0,964
pour Ho=72, alors (1/Ho) = 13,58 Ga (Ga pour milliards d’années),
l’âge réel de l'univers est alors 13,58*0,964=13,09 Ga = 13,09 milliards d’années
 SOURCES
SOURCES
Pour chaque galaxie :
- l’image de la galaxie est extraite du Palomar Observatory Sky Survey
http://archive.stsci.edu/cgi-bin/dss_form
- la distance estimée de la galaxie est extraite de la NED Extragalactic Database)
http://ned.ipac.caltech.edu/forms/d.html
La valeur moyenne est extraite avec l’incertitude associée (standard déviation) et reportée dans le Tableau des galaxies
-le spectre global de la galaxie et la région de la raie d’hydrogène est extrait de :
l’Atlas Spectrophotometrique de Galaxies,
R. Kennicutt, Astrophysical Journal Supplement Series, vol. 79, no. 2, April 1992, p. 255-284,
http://adsabs.harvard.edu/abs/1992ApJS...79..255K
- un échantillon plus complet de 27 galaxies (en anglais) est accessible sous :
http://www.astro.washington.edu/courses/labs/clearinghouse/labs/HubbleLaw/galaxies.html
Liens externes
- base de données extragalactiques (NED Extragalactic Database)
http://ned.ipac.caltech.edu/
- calculateur cosmologique A Cosmology Calculator for the World Wide Web http://www.astro.ucla.edu/~wright/DlttCalc.html
E. Wright (2006) Publ.Astron.Soc.Pac., vol.118, p. 1711
http://arxiv.org/abs/astro-ph/0609593
Cet atelier est librement adapté de la page "Hubble's law : an introductory astronomy lab" de l'université de Washington